COMO SIMPLIFICAR O AMPLIFICAR LOGARITMOS EN EXAMENES DE ADMISION
Si
formas parte del grupo de jóvenes,
generalmente 6 de cada 10 estudiantes,
que tiene dificultades en la comprensión, desarrollo y simplificación de expresiones
logarítmicas y además harás el examen de admisión ¡quédate
a leer todo el Blog y mira los vídeos sugeridos!
Dado
que entre las temáticas comunes que se
evalúan, explícita o implícitamente, en los exámenes de admisión es el de la simplificación o amplificación de expresiones logarítmicas, se
vuelve imperativo saber reducir expresiones
logarítmicas o determinar logaritmos
equivalentes en exámenes de admisión de matemática que aplican ciertas universidades
como mecanismo de selección de sus estudiantes.
Me he
dado a la tarea de encontrar alternativas para -entre otros tópicos, los cuales
encontrarás a la derecha de éste blog- determinar
logaritmos equivalentes, realizar la simplificación
o amplificación de expresiones logarítmicas en los ejercicios propuestos en
exámenes de admisión; con estrategias
sencillas, comprensibles y aplicables. Es decir, lograr acertar con la opción correcta,
prácticamente sin necesidad que tú sepas simplificar logaritmos. Por
supuesto, las estrategias que se abordan en este Blog y mi canal de Youtube, no son únicas y debes considerar la aplicación
de estas según el tiempo que dispongas para dar respuesta a cada pregunta o problema matemático del
examen de admisión -El tiempo, por pregunta, ejercicio o problema, está en el
intervalo de 1 a 5 minutos, dependiendo de la Universidad-. Además, considera
el hecho si te permiten o no el uso de la calculadora en la prueba de admisión; tus habilidades
para realizar operaciones con logaritmos y cálculo de logaritmos. Todo esto, a
partir de las disposiciones administrativas de cada Universidad.
Mi
objetivo, entusiasmo y misión es ayudar a
todos aquellos jóvenes que aspiran ingresar
a la Universidad, pero que la matemática no es su fuerte (por lo que las estrategias
que verás acá son para facilitarte el enfrentar exitosamente el examen de
admisión, no para jóvenes que
estudian en la Universidad. Aunque algunos jóvenes universitarios me han
comentado que, en situaciones de logaritmos muy complejos, han utilizado estas
estrategias para superar ejercicios semejantes en sus pruebas y exámenes
ordinarios o extraordinarios).
Es
posible que los individuos con mediano o mucho conocimiento matemático
critiquen mi visión; pero, sólo quiero ayudar
al(la) futuro(a) enfermero(a), pedagogo(a), sociólogo(a), periodista, etc. a
realizar el sueño de ingresar a la
Universidad. Imagina el siguiente escenario hipotético: Un(a) joven se convertirá en un(a) extraordinario(a)
periodista de llegar a tener la oportunidad de estudiar periodismo; pero,
producto que no tiene grandes habilidades matemáticas falla en su examen de
admisión de matemáticas y no logra ingresar a la Universidad… ¡sería una pena! Quien
sienta que no necesita de las estrategias que acá se discutirán, por favor,
sólo abandone el Blog y siga con su búsqueda en otro sitio web.
Antes
de entrar en detalle con cada una de las estrategias, debemos analizar un asunto
importante. Algunos(as) jóvenes (quizás te pase a ti) no comprenden con
exactitud qué es lo que se pide realizar, encontrar, calcular, etc. en un ejercicio o problema matemático planteado.
Una de las posibles razones es la falta de dominio de la terminología
matemática; por tal razón, daré algunos términos o frases que, en lo general, te
ayudarán a comprender cuándo se pide simplificar o amplificar expresiones logarítmicas en un ejercicio. Frases o expresiones como:
“La simplificación de la expresión (que contiene logaritmos)…es”,
“al simplificar la expresión (conteniendo logaritmos)… se obtiene”, “la
expresión (logarítmica) equivalente a…”, “hallar el equivalente a (expresión
logarítmica)…”, “cuál es la expresión equivalente a (expresión logarítmica)…”,
“al amplificar (expresión logarítmica), se obtiene:…” entre
otros, son las expresiones, frases o términos más comunes bajo los cuales se
redactan los ejercicios vinculados con la simplificación o amplificación de
expresiones logarítmicas en los exámenes de admisión de matemática.
Obviamente, a medida que practiques, realizando reducción o amplificación de
expresiones logarítmicas utilizando las estrategias que te ofrezco, irás
dominando más este asunto.
DETERMINANDO LA EQUIVALENCIA DE EXPRESIONES
LOGARITMICAS
ESTRATEGIA 1. SUSTITUCION NUMERICA
Esta
estrategia se basa en:
1. Las
preguntas, ejercicios o problemas de los exámenes
de admisión tienen opciones; esto implica, que la respuesta correcta de lo
que se pide hallar, encontrar, calcular, etc., ha de estar en una de las
opciones. Se que es obvio, extrañamente, la mayoría (de los que la matemática
no es su fuerte) no utiliza este recurso a su favor cuando se enfrenta a un examen de
admisión con opciones.
Por ejemplo, si en un problema se
pide determinar el área acotada por una función y los ejes del plano cartesiano,
debes estar seguro de que dicha área está en una de las opciones. Te puede
interesar el siguiente vídeo
2. Cualquier
expresión logarítmica que sea igual a otra expresión logarítmica, también deben
ser numéricamente iguales.
Por ejemplo, si
Numéricamente, las dos expresiones,
tanto
como
han de ser iguales.
Para verificar la igualdad numérica,
asignemos un valor a “x” (al escoger el valor, ten cuidado de que el cálculo
realizado en el argumento no resulte una cantidad negativa, ni cero). Por eso
escogeré, por ejemplo, x = 3.
Al sustituir el valor (x = 3) en
obtenemos
(en lugar de “x” he escrito el 3).
Ahora, hacemos las operaciones
contenidas en el argumento
Realizamos las operaciones contenidas en el argumento, cuidando la jerarquía de operaciones
al simplificar el argumento (extraer mitad al 2 y 256) se obtiene
Como puedes observar, cuando x = 3, el valor numérico de
también es -7. Lo cual evidencia la equivalencia
3. Esta
estrategia la puedes aplicar para determinar cualquier simplificación,
amplificación o equivalencia de expresiones logarítmicas. Observación: Toma en
cuenta que es necesario que en el ejercicio te pidan -explícita o
implícitamente- simplificar, amplificar o determinar una expresión logarítmica
equivalente. Para fortalecer el uso de la estrategia échale un vistazo a
este vídeo
EJERCICIOS POR PRACTICAR
ESTRATEGIA: SUSTITUCION NUMERICA PARA DETERMINAR EQUIVALENCIA DE EXPRESIONES
LOGARITMICAS
Acierta con la opción correcta
utilizando la estrategia sugerida. Al practicar con varios ejercicios,
mejorarás el dominio de la estrategia y reducirás el tiempo en hacer los
cálculos. ¡Ánimo!
OBSERVACIONES FINALES
1. Existe
la posibilidad, al utilizar la estrategia numérica para determinar logaritmos
equivalentes, que más de una opción tenga el mismo valor numérico de la expresión logarítmica dada en el
ejercicio. Por tanto, si eso llegara a ocurrir, lo que debes hacer es escoger
otros valores para las variables contenidas en los logaritmos y repetir el
procedimiento en su totalidad.
2. Al
seleccionar los valores que sustituirás por las variables (letras), ten la
precaución de que, al realizar los cálculos en el argumento de cada logaritmo,
los resultados particulares (en cada argumento) no resulten ser ceros ni
negativos. Si eso ocurre (ceros o negativos en el argumento) escoge otros
valores para las variables (letras). Por ejemplo, si el argumento de algún
logaritmo es (x – 5) no escojas un valor para “x” menor o igual a 5; si el
argumento es (x + 9) no selecciones valores menores o iguales a -9 (son
ejemplos de números menores que nueve: -9.1, -10, -20, etc.)
3. Si
en el examen
de admisión no te permitirán el
uso de la calculadora, esta estrategia no es tan viable, puedes considerar la
estrategia que comparto en la sección de abajo. Pero, si aún deseas seguir
adelante con esta estrategia, considera lo siguiente:
a. Aplícala
en situaciones de expresiones logarítmicas sencillas, las cuales son comunes en
pruebas de admisión en las que no permiten el uso de la calculadora.
b. Al
escoger los valores, te sugiero escojas valores que generen resultados, en el
argumentos de los logaritmos, que permitan calcular logaritmos fácilmente (como
puedes observar en el ejemplo que desarrollé); es decir, si el logaritmo es de
base 3, procura escoger valores (para las letras) que generen resultados (en el
argumento) potencias de 3 (3, 9, 27, 81, etc.); si el logaritmo es de base 7,
potencias de 7 (7, 49, 343, etc.). Y así sucesivamente
4. Si
en el examen te permitirán el uso de la calculadora, escoger valores tales como
el 11, 13, 17, 19 vuelve prácticamente improbable que ocurra lo explicado en el
numeral 1 de las observaciones finales.
5. Si
la expresión logarítmica contiene más de una variable/incógnita (letra), te
sugiero escoger valores diferentes para cada una de las letras.
ESTRATEGIA 2. UTILIZANDO PROPIEDADES
Para
utilizar esta estrategia debes considerar los siguientes aspectos:
1. La definición de
logaritmo es:
Donde:
a: Se
llama base de logaritmo.
x: Se
llama argumento del logaritmo.
n: Se
llama logaritmo.
esto quiere decir que
la base del logaritmo debe ser un número
mayor que cero y no puede ser igual a 1.
Ejemplos:
log2
8 = 3 porque
23 = 2*2*2
= 8
Acá,
la base del logaritmo es 2, el argumento es 8 y el logaritmo es 3.
log7
49 = 2 porque
72 = 7*7
= 49
Acá,
la base del logaritmo es 7, el argumento es 49 y el logaritmo es 2.
log5
625 = 4 porque
54 = 5*5*5*5
= 625
1. Propiedades de
los logaritmos:
a. El logaritmo de un producto equivale a la suma de los logaritmos.
Esto se puede expresar así:
En
retrospectiva, la
suma de los logaritmos equivale al logaritmo del producto.
b. El logaritmo de un cociente equivale a la diferencia de los
logaritmos;
específicamente: el logaritmo del dividendo menos el logaritmo del divisor.
Esto se puede expresar así:
En
retrospectiva, la
diferencia de logaritmos equivale al logaritmo del cociente, dicho
cociente debe expresarse así: El argumento del minuendo entre el argumento del
sustraendo.
c. Logaritmo de una potencia equivale al producto del exponente por
el logaritmo de la base de la potencia,
se expresa así:
En
retrospectiva, una
expresión (numérica o algebraica) que multiplique a un logaritmo, es exponente
para el argumento del logaritmo.
A
partir de la definición y propiedades de los logaritmos se deriva lo siguiente:
a. El logaritmo de una potencia en la cual la base del logaritmo es
igual a la base de la potencia, el logaritmo es el exponente de la potencia, lo
cual se puede expresar así:
b. El logaritmo de cero no existe, es decir:
c. El logaritmo de cantidades negativas no existe, por ejemplo:
d. El logaritmo de 1 es cero, por ejemplo:
Para
utilizar esta estrategia, además de dominar plenamente las propiedades de los
logaritmos, es necesario dominar la factorización de polinomios, propiedades de
la radicación, racionalización, operaciones con polinomios y propiedades de la potenciación.
Ejemplo. Simplificar la expresión
Lo
primero que debemos apreciar es que en
Como el 5 multiplica al logaritmo, podemos ubicarlo como
exponente en el argumento, de la siguiente forma:
Podemos
observar que el dividendo x2 – 1 es
una diferencia de cuadrado perfectos, por lo que factorizaremos. Recordando que
la diferencia de cuadrados equivale al producto de la suma de las raíces
cuadradas de los términos del binomio, por la diferencia de las mismas raíces.
Primero
extraemos las raíces cuadradas de ambos términos
Ahora bien, el denominador del argumento se puede expresar -de acuerdo con la definición de la potenciación- como sigue:
(x + 1)5 = (x + 1)(x + 1)(x + 1)(x +
1)(x + 1)
Y dado
que en el dividendo se encuentra un (x + 1),
éste se puede simplificar con uno de los (x + 1) que
se encuentran en el divisor. El logaritmo toma la forma:
En
conclusión
Como
ya lo sabíamos.
Obviamente,
a quien no le gusta la matemática le da pereza ver la estrategia de simplificar
logaritmos utilizando propiedades. Pero, si tu sueño es ingresar a la
Universidad, debes ser tenaz, estar determinado a conquistar tu sueño y
dispuesto al sacrificio. A la larga, tu decides cuál
de las dos estrategias prefieres usar.
Para
practicar la estrategia, puedes hacerlo con los ejercicios planteados arriba.
Si al resolver los
ejercicios matemáticos propuestos arriba, aún llegas a tener dudas sobre haber
determinado la opción correcta, puedes enviarme la opción (de cada ejercicio
propuesto) que tú consideras correcta. Para contactarme, dejo las formas para
hacerlo al final de esta página. Yo te responderé en el menor tiempo posible
¡Ánimo!
Siempre
estoy anuente y dispuesto a recibir:
1. Crítica
constructiva (crítica sobre el enfoque de contenido y estrategias, que me
ayuden a mejorar).
2. Ayuda
con:
a) Traducciones
a otros idiomas de este blog y los vídeos de mi canal en Youtube.
b) Enviarme
tipos de ejercicios, problemas o contenido no abordados en mi blog o canal deYoutube.
c) Con
el diseño de miniaturas en mis vídeos de Youtube.
3. Sugerencias
en el abordaje de la temática (que tan clara está explicada la estrategia para determinar expresiones logarítmicas
equivalentes).
4. Cualquier
otro asunto que consideres necesario comunicarme con ánimo de mejorar contenido
del blog y vídeos de mi canal.
Para contactarme:
Visita mi canal y sitios web en construcción:
COMPARTE ENLACE DE ESTE BLOG, MI CANAL DE YOUTUBE Y VIDEOS POR MEDIO DE
TUS REDES SOCIALES. Y AVISA A TUS AMIGOS Y CONOCIDOS DE LA EXISTENCIA DE ESTAS
ESTRATEGIAS. SALUDOS.
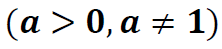
No hay comentarios:
Publicar un comentario